Partes del especial «El modelo estándar y el bosón de Higgs»
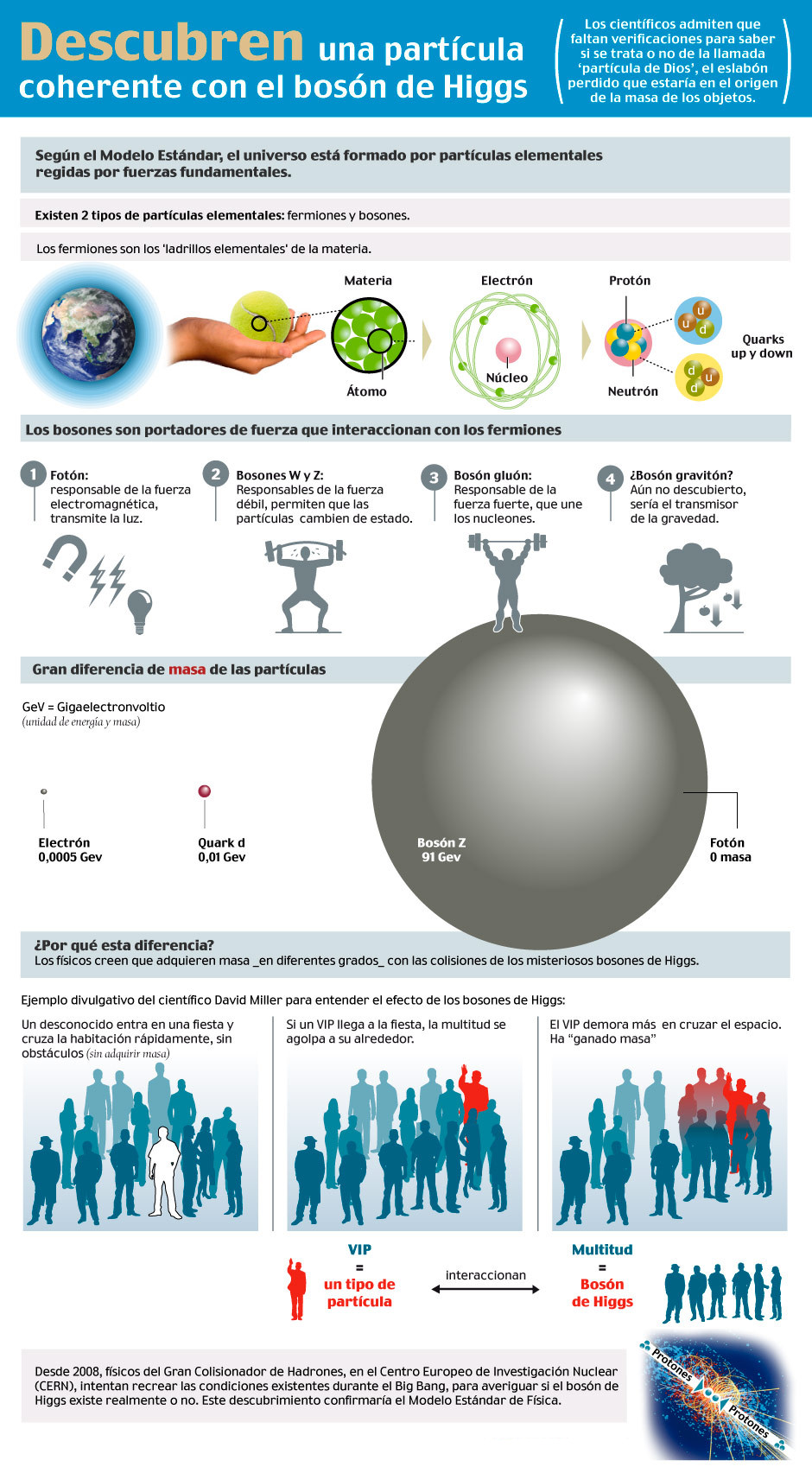
Parte 1: El Modelo Estándar
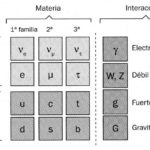
Parte 2: Constituyentes básicos de la materia
Parte 3: Interacciones básicas
Parte 4: Simetrías básicas
Parte 5: Masa contra simetría
Parte 6: El mecanismo de Higgs
Parte 7: Una imagen sencilla
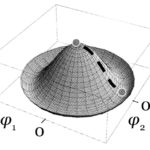
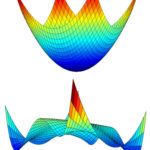
Parte 8: Ruptura espontánea de la simetría
Parte 9: Ruptura electrodébil
Parte 10: Al comienzo del universo…
Las simetrías del Modelo Estándar describen a la perfección las interacciones básicas, pero tienen un problema: se llevan muy mal con que las partículas tengan masa. Para entenderlo, supongamos una partícula cualquiera con masa, por ejemplo un electrón o un quark. Representemos su campo por la letra griega ψ (psi). La evolución del campo ψ está dictada por una cierta ecuación.

Sin entrar en detalles de esta ecuación, vamos a fijarnos solo en el trozo de la misma que contiene la información de que este campo corresponde a una partícula con masa. Ese trozo se suele llamar «término de masa» y tiene esquemáticamente la siguiente forma:
M × ψ2
donde m es la masa de la partícula. Cualquier partícula con masa tiene en su ecuación de evolución un término semejante al que acabamos de ver. El problema es que esta expresión no es invariante bajo una transformación del campo ψ.
Si modificamos el valor del campo ψ también lo hace su valor al cuadrado, ψ2, y por tanto el término de masa que hemos escrito arriba. Así que el término de masa estropea la simetría interna de las ecuaciones. Hay que decir que este problema afecta a todas las partículas con masa, y muy especialmente a los bosones W y Z, es decir, los mediadores de la interacción débil. La simetría interna exige, contra toda evidencia, que las partículas han de tener masa nula. ¿Es que hemos de renunciar a la simetría de las ecuaciones?
Si no hubiera más remedio, por supuesto. El problema es que, como ya mencionamos, si las ecuaciones dejan de ser simétricas, se vuelven inconsistentes. Describir con precisión esa inconsistencia requeriría el uso de conceptos demasiado técnicos, pero podemos decir que la inconsistencia se deja ver especialmente cuando uno calcula la probabilidad de que suceda algún proceso en el que intervengan los bosones mediadores masivos, es decir los W y Z.
Por ejemplo, usando las reglas de la Teoría Cuántica de Campos uno puede calcular la probabilidad de que dos bosones W, lanzados uno contra otro, choquen. Por lógica, la máxima probabilidad imaginable es igual a uno, lo que significaría que el choque es seguro. Sin embargo, al realizar el cálculo, uno encuentra que, si la energía es suficientemente alta, ¡la probabilidad es mayor que uno!
Por tanto, aquí tenemos un problema teórico que trajo a los físicos de cabeza durante bastantes años: necesitamos que las ecuaciones sean simétricas para que no haya inconsistencias. Esto significa que todas las partículas han de tener masa nula, en particular los bosones W y Z. Pero esto contradice la evidencia experimental. ¿Cómo reconciliar la imprescindible simetría de las interacciones con la masa de las partículas?