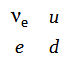Partes del especial «El modelo estándar y el bosón de Higgs»
Parte 1: El Modelo Estándar
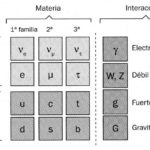
Parte 2: Constituyentes básicos de la materia
Parte 3: Interacciones básicas
Parte 4: Simetrías básicas
Parte 5: Masa contra simetría
Parte 6: El mecanismo de Higgs
Parte 7: Una imagen sencilla
Parte 8: Ruptura espontánea de la simetría
Parte 9: Ruptura electrodébil
Parte 10: Al comienzo del universo…
El mecanismo de Higgs ha sido posiblemente la propuesta más ingeniosa para resolver el problema de cómo dar masa a las partículas. A pesar de su nombre, lo cierto es que fueron varios físicos, además de Peter Higgs, los que contribuyeron a su formulación. El mecanismo había sido en esencia propuesto por Philip Anderson en 1962 en un contexto diferente.


Peter Higgs, a la izquierda. Philip Anderson, a la derecha.
En 1964, Robert Brout y François Englert propusieron el mecanismo en el contexto de la física de partículas. Algo después, en el mismo año de 1964, Peter Higgs descubrió que implicaba la existencia de una nueva partícula (el bosón de Higgs). Al poco tiempo, otros autores, como Guralnik, Hagen y Kibble, propusieron la misma idea de forma independiente. Como sucede a menudo en ciencia, es difícil atribuir avances importantes a un autor en exclusiva. En cualquier caso, ¿en qué consiste el mecanismo de Higgs?
Para ser más concretos, consideremos nuevamente el campo ψ, que representa un electrón o un quark. Sabemos que cuando hacemos una transformación asociada a una de las simetrías básicas del Modelo Estándar, este campo se transforma. La transformación consiste en que el valor del campo se multiplica por un número, o sea ψ → ψ × q (en vez de la transformación aditiva que escribimos antes ψ → ψ + q, pero esto no es lo importante). Por tanto, su término de masa cambia en la forma:
m × ψ2 → m × ψ2 × q2
Supongamos ahora que este indeseable término de masa (indeseable porque no es invariante) no existe. En su lugar escribimos un término que involucra un campo adicional, al que llamaremos H y que sustituye a la masa (este es el «campo de Higgs»). Así pues, en vez de m × ψ2 escribimos:
H × ψ2
Si ahora suponemos que el campo H se transforma bajo la simetría en la forma H → H/q2, resulta que la combinación que acabamos de escribir queda invariante, ya que la transformación de H compensa exactamente la transformación de ψ.
H × ψ2 → H × ψ2
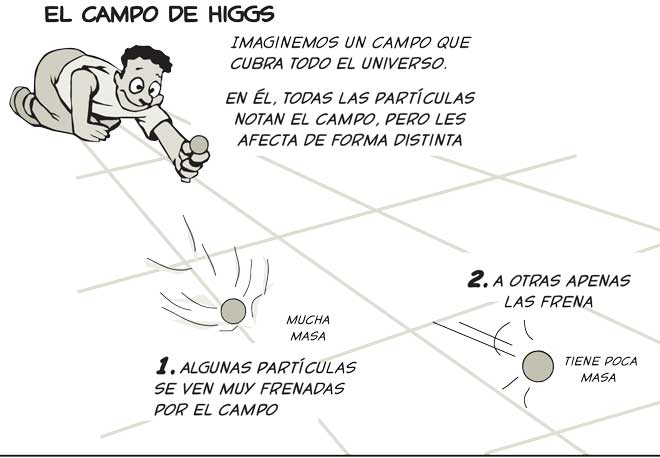
Esto es satisfactorio, pero el término H × ψ2 no es un término de masa, sino de interacción entre el campo ψ y el campo H. Ahora viene la hipótesis revolucionaria. Supongamos que el universo está lleno del campo H. En otras palabras, en cualquier punto del universo, incluso en los espacios vacíos, el campo H tiene un valor distinto de cero, llamémoslo H0. Esto puede resultar antiintuitivo, ya que significa que el vacío no está realmente vacío, sino lleno de un campo invisible.

Más adelante volveremos sobre este punto. Ahora lo importante es fijarse en que si esto es así, por raro que parezca, entonces ese valor H0 hará en la práctica el papel de masa de la partícula ψ. Para ver esto más claro, imaginemos que el valor del campo en el vacío, H0, es como el nivel del agua de un lago cuando está tranquilo.
Las pequeñas alteraciones de ese nivel, debido a agitaciones del agua, podemos llamarlas h. Así pues H = H0 + h. Notemos que H0 es un valor fijo, mientras que h es algo cambiante y dinámico, como un campo ordinario. Usando esta descomposición podemos escribir el término anterior como:
H × ψ2 = H0 × ψ2 + h × ψ2
La observación crucial es que el primer término del miembro de la derecha, H0 × ψ2, es exactamente como un término de masa, ocupando H0 el papel de m. El segundo término de la derecha, h × ψ2, representa una interacción entre el campo ψ y el campo h, es decir, una interacción de la partícula ψ (electrón, quark o lo que sea) con las excitaciones del campo H. Pues bien, esas excitaciones (el campo h) son el famoso bosón de Higgs.
Notemos que todo esto ha surgido de un término, H × ψ2 que era invariante bajo la simetría. Por tanto, la teoría sigue siendo simétrica y gracias a ello se curan las inconsistencias que mencionábamos hace algunas páginas. El término de masa que hemos generado parece estropear la simetría, pero en realidad la simetría sigue estando ahí, solo que camuflada.
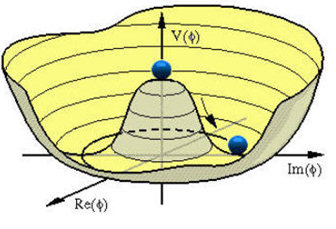
Y lo que la camufla es el hecho de que el campo H, que tiene un valor fijo en el vacío, es a la vez un campo que se transforma imaginariamente bajo la simetría interna de la teoría (recordemos que lo hace en la forma H → H/q2). Esa es la magia del mecanismo de Higgs.
Puede parecer una idea descabellada, ya que implica la existencia de un campo invisible que lo llena todo. Lo asombroso es que (si se confirma que el bosón recién descubierto tiene las propiedades del bosón de Higgs) la naturaleza parece estar dando la razón a la idea «descabellada» de Brout, Englert y Higgs.
¿Por qué tiene cada partícula una masa diferente? Según este esquema, porque interacciona con el campo H con una intensidad diferente. Por ejemplo, para el electrón la interacción con el campo H es proporcional a una constante llamada «acoplo de Yukawa» del electrón, ye. Así pues, para el electrón escribimos:
ye × H × ψ2 = ye × H0 × ψ2 + ye × h × ψ2
Su masa es por tanto ye × H0. Desde esta perspectiva, el electrón tiene una masa pequeña porque su acoplo de Yukawa, ye, es pequeño (y también será pequeña su interacción con el bosón de Higgs, o sea, el último término de la ecuación anterior). Otras partículas tienen acoplos de Yukawa más grandes y por tanto masas más grandes.
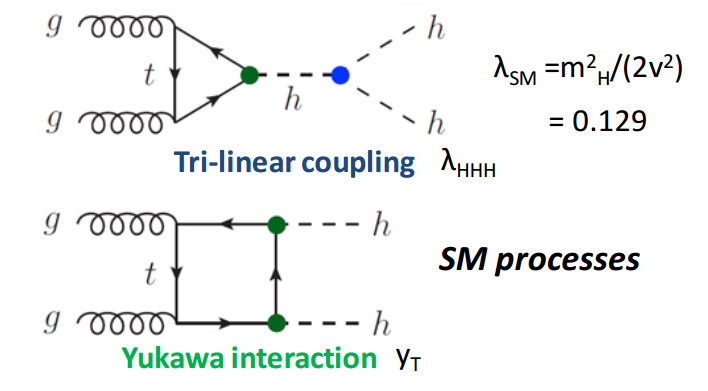
¿A qué se debe que cada partícula tenga un acoplo de Yukawa diferente, es decir, que interaccionen con mayor o menor intensidad con el campo de Higgs? No lo sabemos. Aquí nos encontramos de nuevo con el problema del sabor mencionado anteriormente. El mecanismo de Higgs nos ayuda a entender por qué las partículas tienen masa, pero no nos dice cuánto vale su masa.
La última afirmación tiene una excepción extremadamente interesante. La interacción del campo de Higgs con los bosones W y Z se debe exclusivamente a la interacción débil (recordemos que son las partículas mensajeras de la misma) y por tanto está fijada de antemano. En consecuencia, la masa del bosón W es el producto del acoplo de la interacción débil (que es perfectamente conocido) por H0.
Como, por otra parte, sabemos experimentalmente la masa del W, esto nos permite deducir cuánto vale la cantidad H0, que resulta ser H0 = 246 GeV. Para el bosón Z también conocemos su acoplo con el Higgs. Es ligeramente distinto al acoplo del W, pero lo importante es que también está fijado de antemano por la interacción débil.
Así que, usando el valor de H0 que acabamos de establecer (o sea H0 = 246 GeV), podemos deducir la masa del bosón Z. El resultado es unos 91 GeV. El bosón Z fue descubierto en el CERN en 1983, precisamente con la masa predicha por la teoría. Este hallazgo se considera el más importante realizado por el CERN… hasta el descubrimiento del propio bosón de Higgs, y da un gran respaldo a todo el esquema teórico.
Para terminar esta sección, un apunte técnico: las partículas asociadas al campo del Higgs han de tener espín cero. De otra forma, al tomar el campo un valor en el vacío, establecería una orientación privilegiada en él (la de su momento angular o «giro» intrínseco), y la experiencia demuestra que el vacío no tiene orientaciones privilegiadas. Por ello, el bosón de Higgs que se ha buscado en el LHC ha de tener espín cero, una predicción importante del Modelo Estándar que aún hay que confirmar.
El mecanismo de Higgs suscita algunas cuestiones. Si el vacío está lleno de un campo, ¿entonces es que ya no es auténtico vacío? ¿Qué es lo que provoca que el universo esté lleno de este campo misterioso? ¿Siempre fue así (y lo seguirá siendo)? Iremos encontrando algunas respuestas en próximos posts.