Partes del especial «El modelo estándar y el bosón de Higgs»
Parte 1: El Modelo Estándar
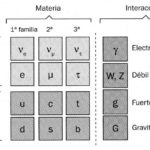
Parte 2: Constituyentes básicos de la materia
Parte 3: Interacciones básicas
Parte 4: Simetrías básicas
Parte 5: Masa contra simetría
Parte 6: El mecanismo de Higgs
Parte 7: Una imagen sencilla
Parte 8: Ruptura espontánea de la simetría
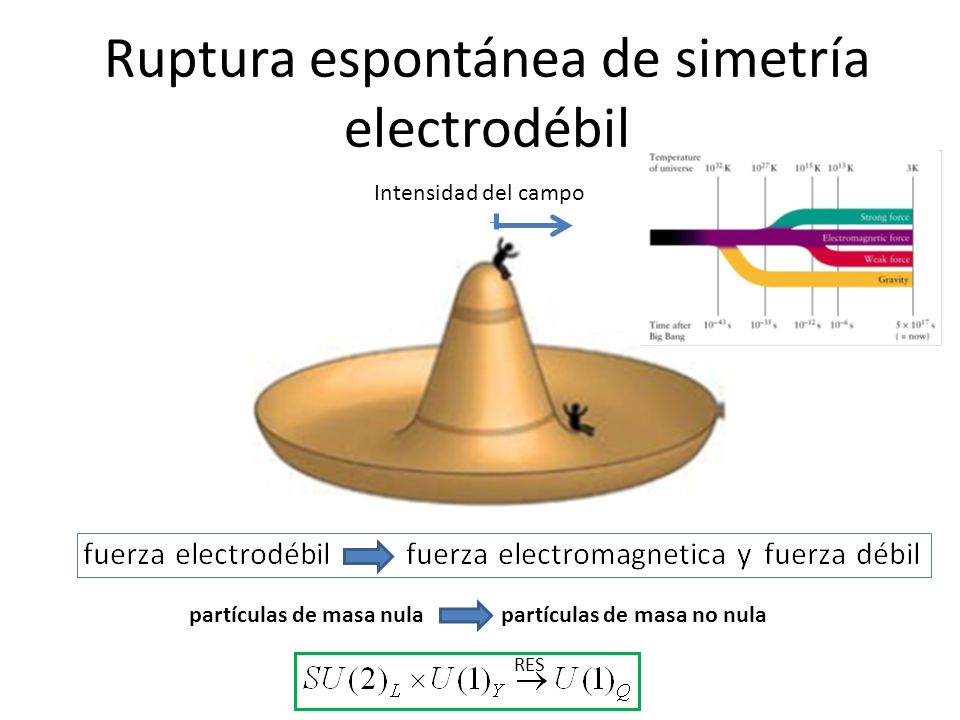
Parte 9: Ruptura electrodébil
Parte 10: Al comienzo del universo…
Antes hemos dicho que el mecanismo de Higgs no estropea la simetría de partida, pero hace que quede camuflada. Este hecho se conoce como ruptura espontánea de la simetría, un nombre desafortunado, ya que sugiere que la simetría se ha estropeado, cuando lo cierto es que sigue estando ahí, aunque no lo parezca.
Desde que fue propuesto por Yoichiro Nambu en 1960, el concepto de ruptura espontánea ha sido central en la física de partículas, tanto en la formulación del Modelo Estándar como en los modelos que se han propuesto más allá de él. Merece la pena por ello que profundicemos un poco más en esta idea.
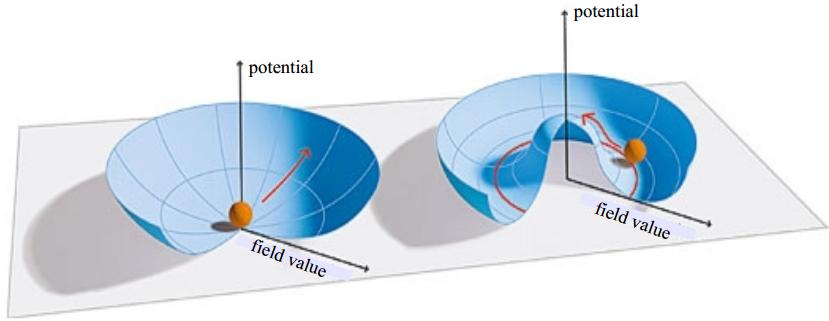
El proceso de ruptura espontánea es equivalente al que tiene lugar si nos subimos a la cúspide de una cúpula semiesférica y nos dejamos deslizar por su superficie hasta la base. Cuando estamos arriba, observamos el aspecto simétrico de la cúpula (invariante bajo rotaciones en torno a su eje vertical).
Cuando caemos abajo, ya no observamos esa simetría, aunque sepamos que está ahí. Lo que observamos es que a un lado tenemos una superficie curva que se eleva, y que al otro lado no hay nada. Este es el proceso que experimenta el campo de Higgs cuando toma un valor en el vacío.
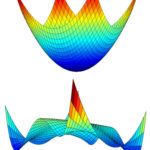
Para ver esto mejor, supongamos por un momento que existen dos campos φ1 y φ2, que pueden tomar valores cualesquiera. Normalmente, los campos almacenan energía. Según el valor que tomen, almacenan más o menos. Se podría pensar que cuanto más grande es el valor del campo, mayor es la energía almacenada, pero no tiene por qué ser así. Supongamos, por ejemplo, que la energía almacenada para cada valor de φ1 y φ2 es tal como muestra la siguiente figura:
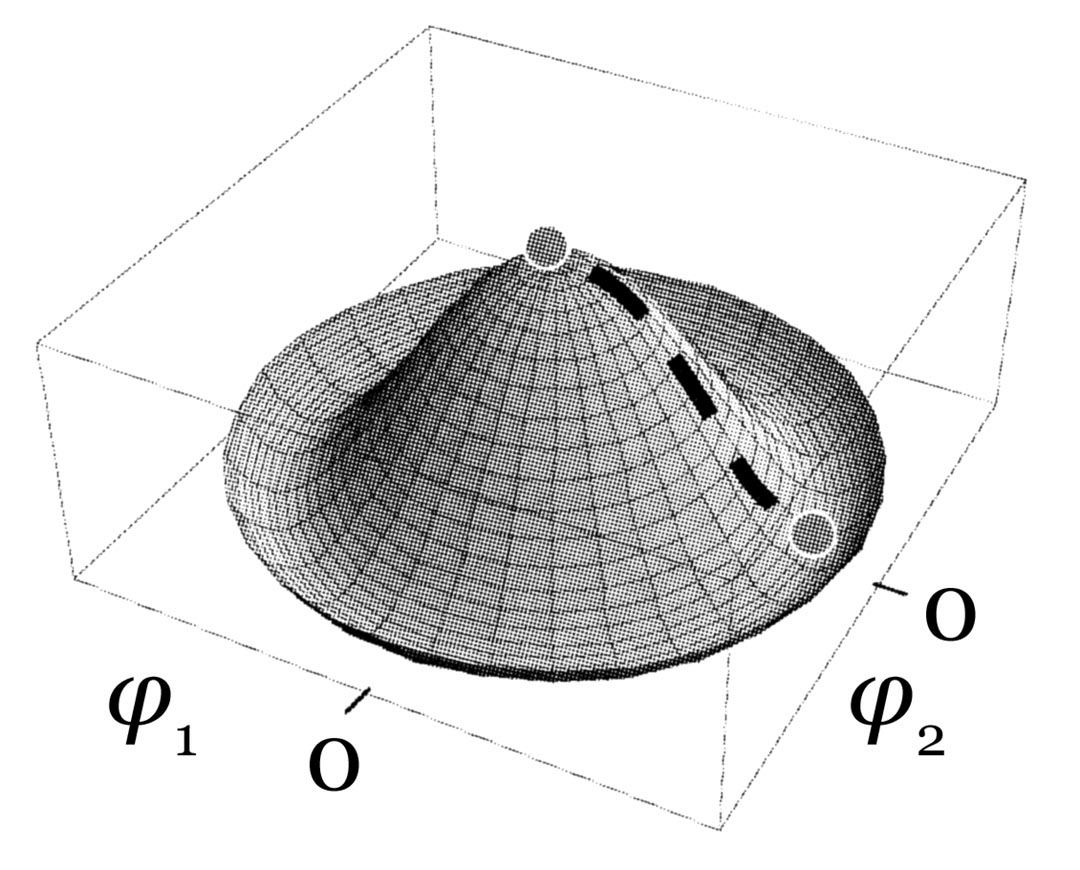
La altura de la superficie dibujada representa la energía almacenada para cada valor posible de φ1 y φ2. Esto es lo que se llama el potencial asociado a los campos φ1 y φ2. En nuestro ejemplo, el potencial es máximo cuando los dos campos toman el valor cero (la cúspide de la cúpula).
Al alejarnos de ese valor, el potencial disminuye, aunque luego vuelve a aumentar. Naturalmente, el potencial asociado a los dos campos φ1 y φ2 no tiene por qué tener el aspecto que hemos dibujado. Por ejemplo, el punto central, φ1= 0, φ2 = 0, podría haber correspondido a un mínimo del potencial, en vez de a un máximo. No entraremos ahora en las razones físicas que pueden causar que el potencial sea como el de la figura.
Pero está claro que, si esto es así por el motivo que sea, de forma natural los campos φ1 y φ2 se alejarán del punto cero hasta terminar con un valor que minimice el potencial, es decir, algún punto del canal circular que rodea la cúspide del potencial. Esto está representado en la figura por una bola que se desliza por la ladera del potencial hasta dicho canal. La posición de la bola simboliza el valor de los campos φ1 y φ2 en un momento dado.
Pensemos en lo que significa este proceso físicamente. Partimos de una situación en la que los campos φ1 y φ2 tienen valor cero; es decir, no hay campos φ1 y φ2 que llenen el universo. Pero luego, de forma espontánea, estos toman un valor distinto de cero: el vacío se ha «llenado» de ellos. Pero ¿podemos seguir llamando legítimamente «vacío» al nuevo estado de cosas? Al fin y al cabo ahora hay dos campos, φ1 y φ2, que están ocupando todo.
Consideremos por un momento el concepto de vacío. Intuitivamente, un recipiente estará vacío cuando quitemos todo lo que hay en su interior, incluido el aire. Pero quitar cosas significa quitar energía; recordemos que la materia no es más que energía concentrada, según nos enseñó Einstein. Por tanto, el vacío se corresponde con el estado de mínima energía, y por ello es legítimo llamar vacío a la nueva situación, ya que es la de mínima energía, aunque φ1 y φ2 tomen un valor no nulo.
Notemos por otro lado que el potencial que hemos dibujado para los campos φ1 y φ2 tiene de partida una simetría, que puede apreciarse en la figura anterior. Concretamente, si modificamos los valores de φ1 y φ2 de forma que nos movamos imaginariamente a lo largo de un círculo cualquiera alrededor del punto cero, entonces la energía no cambia; el aspecto del potencial sigue siendo el mismo.
Esta simetría es evidente si nos situamos mentalmente en la cúspide del potencial, es decir en una situación física en la que los campos φ1 y φ2 tienen valor cero. Esto corresponde a colocarse en la cima de la cúpula semiesférica de nuestro ejemplo anterior. Pero en cuanto nos movamos hacia abajo (o sea, cuando los campos φ1 y φ2 tomen un valor), la simetría se habrá roto espontáneamente; es decir, dejará de ser evidente.
Este proceso que acabamos de ilustrar es exactamente el que le sucede al campo de Higgs. En realidad, el campo de Higgs, H, es un conjunto de cuatro campos (llamados componentes de H). Y, para dos de ellos, el potencial es exactamente como el que hemos representado. Así que podemos imaginar que los campos φ1 y φ2 de la figura son dos de las componentes del campo de Higgs auténtico.
Ahora pensemos lo siguiente: sabemos que las partículas físicas están asociadas a excitaciones de los campos. Cuando estamos en el nuevo vacío (o sea, la bolita de la figura está situada en el canal circular), hay dos formas en que podemos alterar los campos φ1 y φ2. La primera es moviéndonos a lo largo del canal circular. Esto no cuesta energía, ya que el canal está todo él a la misma altura (mismo potencial).
Por tanto esta excitación corresponde a una partícula sin masa, llamada bosón de Nambu-Goldstone (no confundir con el bosón de Higgs). Cuando la simetría es del tipo local, este bosón de Nambu-Goldstone desaparece como tal partícula independiente. La razón es que pasa a ser una componente adicional de la partícula mediadora de la interacción. Este es un aspecto bastante técnico en el que no podemos profundizar más.
Digamos que el bosón de Nambu-Goldstone es «tragado» de alguna forma por la partícula mediadora de la interacción rota, que ahora pasa a tener masa. Mencionemos de paso que solo las partículas mediadoras asociadas a simetrías rotas adquieren masa. Las demás partículas mediadoras siguen sin masa. La propia simetría que las origina les prohíbe adquirirla.
La segunda excitación posible de los campos φ1 y φ2 consiste en moverse perpendicularmente al canal circular de la figura anterior, lo cual exige trepar por la ladera del potencial, y por tanto cuesta energía. Por ello, la partícula correspondiente tiene masa. Y esa partícula con masa se trata del famoso bosón de Higgs, una consecuencia necesaria de todo este mecanismo.