Partes del especial «La masa en la ciencia»
Parte 1: Teorías de Newton y Einstein
Parte 2: Un átomo al microscopio
Parte 3: Mecánica Cuántica
Parte 4: Masa, espín y simetría
Para finalizar nuestro recorrido histórico por el concepto de masa, vamos a discutir su relación con la idea de simetría. El concepto de simetría, aplicado a las leyes físicas, es una de las nociones centrales en la física de partículas moderna.
En general, una simetría de un objeto es una transformación que lo deja idéntico a sí mismo. Por ejemplo, si rotamos un cuadrado 90° respecto a su centro, la figura resultante será idéntica al cuadrado inicial. Pero cuando hablamos de las leyes físicas, es decir, de las ecuaciones básicas de la naturaleza, hemos de pensar en una transformación matemática de las ecuaciones que las deja idénticas a sí mismas. Pongamos un ejemplo con una ecuación ideal, particularmente simple.
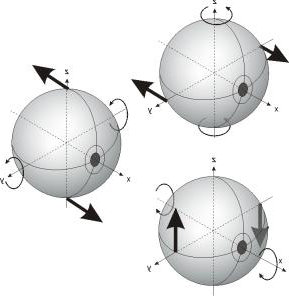
Supongamos una partícula que se mueve con velocidad constante, v, y consideremos la partícula en dos instantes distintos, t1 y t2. La distancia, d, recorrida entre esos dos instantes será el producto de la velocidad por el intervalo de tiempo entre ellos. Podemos escribir:
d = v × (t2 − t1)
Supongamos ahora que alteramos los valores de t1 y t2, añadiéndoles una misma cantidad, q:
t1 → t1 + q
t2 → t2 + q
Está claro que la diferencia t2 − t1 seguirá siendo la misma después de esta transformación y, por tanto, la ecuación inicial quedará invariante. Así que las transformaciones que acabamos de escribir son una simetría de esa ecuación. Por cierto, que este tipo de transformación se llama «traslación temporal», ya que es equivalente a trasladarnos un tiempo q hacia el futuro.
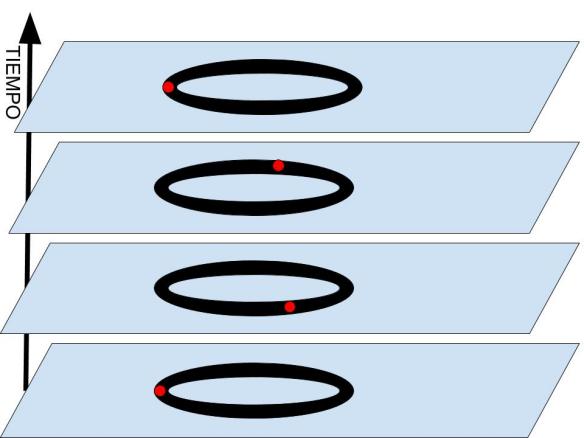
Por ello, el significado de esta simetría es que la ecuación considerada no cambia con el tiempo. Las verdaderas ecuaciones que describen (hasta donde sabemos) el comportamiento de las partículas elementales son más complicadas que la anterior, aunque tampoco demasiado. Y presentan un gran número de simetrías, es decir, transformaciones que las dejan invariantes, entre ellas las traslaciones temporales que acabamos de discutir.
¿Por qué son importantes las simetrías? Aparte de dar elegancia a las ecuaciones, las simetrías tienen implicaciones físicas muy concretas. Se puede demostrar que en muchos casos conducen a la existencia de cantidades que se conservan. Por ejemplo, que las ecuaciones básicas de las partículas sean simétricas bajo traslaciones temporales implica la existencia de una cantidad conservada: la energía. Anteriormente ya dijimos que la masa es en realidad energía concentrada.
Pero ¿qué es la energía? Pues sencillamente una cantidad que se conserva como consecuencia de una simetría básica: que las leyes físicas no cambian con el tiempo. Esta conexión general entre simetrías y cantidades que se conservan es un resultado de enorme trascendencia, descubierto por la gran matemática y física alemana Emmy Noether en 1919, en el contexto de la teoría de campos clásica.
Emmy Noether.

En la física moderna, las simetrías ocupan un lugar fundamental en la explicación de aspectos esenciales de la naturaleza. De forma análoga a las traslaciones temporales, las ecuaciones básicas de las partículas elementales son invariantes bajo traslaciones espaciales y bajo rotaciones, es decir, son las mismas en cualquier punto del espacio y no presentan ninguna dirección privilegiada. Y esto conlleva otras cantidades conservadas: el momento lineal y el momento angular, que se estudian en la Educación Secundaria.
Recordemos ahora que, según la Teoría de la Relatividad Especial, las leyes físicas han de ser las mismas para un observador en reposo y para uno con velocidad constante. Esto implica que las leyes físicas han de ser invariantes bajo las transformaciones que relacionan lo que ven esos dos observadores, lo que significa una nueva simetría. Las transformaciones en cuestión han de ser de tal forma, además, que la velocidad de la luz sea siempre la misma, vista por el observador en reposo o por el que está en movimiento (como dicta la Relatividad Especial).
Esas transformaciones son las llamadas Transformaciones de Lorentz, que están en el corazón de la Teoría de la Relatividad. Podemos imaginar esas transformaciones como la receta para describir de qué manera cambia el aspecto de un fenómeno cuando lo observamos en reposo o montados en un sistema en movimiento.
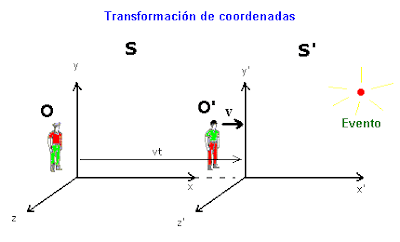
El fenómeno puede que se vea diferente, pero las leyes básicas subyacentes tienen que seguirse viendo y escribiendo igual. Por tanto las Transformaciones de Lorentz han de ser (¡y, por lo que sabemos, lo son!) una simetría de la naturaleza, lo que tiene consecuencias trascendentales, como vamos a ver.
Cuando consideramos una teoría que sea a la vez relativista y cuántica, es decir una Teoría Cuántica de Campos (TCC), resulta que las partículas, es decir las excitaciones elementales del campo asociado, han de estar necesariamente caracterizadas por dos parámetros: la masa y el espín (enseguida aclararemos este último concepto). Esto es una consecuencia directa de la simetría bajo Transformaciones de Lorentz, que fue establecida de forma sistemática y rigurosa por Eugene Paul Wigner en 1938.
Así que si la naturaleza es relativista y cuántica, como parece ser, necesariamente los estados básicos, es decir las partículas elementales, deben poseer un atributo llamado masa, que es la energía que almacena la partícula por el mero hecho de existir. Esa masa puede ser cero o distinta de cero, la TCC por sí sola no permite determinarlo.
Si es cero (como les ocurre a los fotones), la Teoría de la Relatividad obliga a que la partícula se desplace a la velocidad de la luz; pero esa masa igual a cero sigue siendo una propiedad que define a la partícula. Esto nos da una nueva perspectiva sobre la masa: que los electrones o los quarks tengan un atributo llamado masa es algo obligado por la TCC. Falta entender por qué tiene el valor que tiene para cada tipo de partícula.

Por su parte, el espín de una partícula es su momento angular intrínseco, es decir, el «giro» que tiene sobre sí misma por el mero hecho de existir. Podemos imaginarnos las partículas como bolitas con una cierta masa girando sobre sí mismas, igual que la Tierra alrededor de su eje. Esta imagen es útil e intuitiva, pero recordemos que realmente los electrones y los quarks son partículas puntuales (no tienen volumen), por lo que no tiene sentido que giren sobre sí mismos.
Sin embargo, la TCC nos dice que no hay ningún problema para que una partícula puntual tenga un momento angular «intrínseco», que es precisamente el espín. Es más, las partículas han de tener un atributo que es su momento angular intrínseco, aunque este sea cero. Además, la Mecánica Cuántica predice que el espín está «cuantizado», es decir, no puede valer cualquier cosa, sino que es siempre un múltiplo de una cantidad mínima.
En un cierto tipo de unidades, esa cantidad mínima es 1/2. Así, puede haber partículas con espín 0, 1/2, 1, 3/2, 2… Las partículas de espín entero (0, 1, 2…) se denominan bosones, y las de espín semientero (1/2, 3/2…), fermiones. Esto se corresponde perfectamente con lo que se observa en la naturaleza para todas las partículas (sean elementales o no), lo que supuso un gran triunfo de la Mecánica Cuántica.
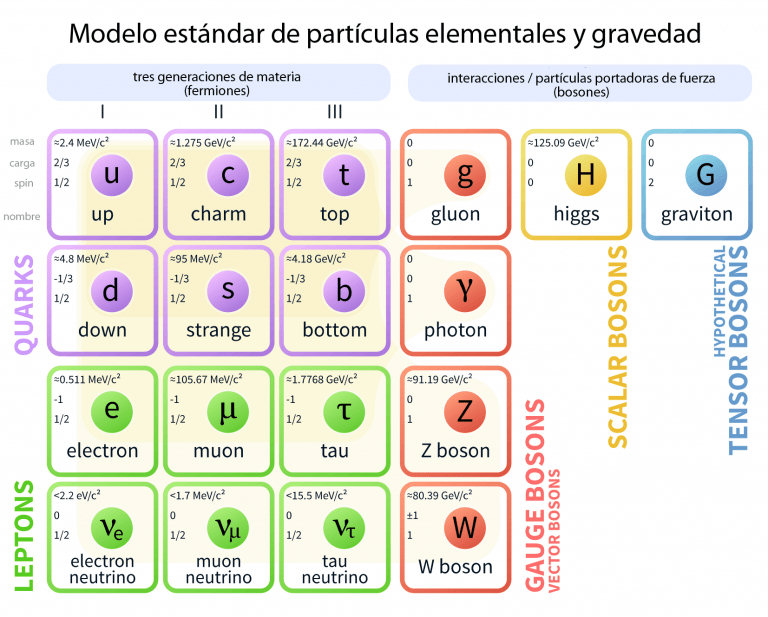
Los electrones y los quarks tienen espín 1/2 (son fermiones). Los fotones y los gluones tienen espín 1 (son bosones). Y el bosón de Higgs que tal vez se haya descubierto en el LHC tiene espín cero. Si se confirma su naturaleza, será la primera partícula elemental (no compuesta) con espín cero. Desde un cierto punto de vista, el espín está en un estatus parecido a la masa. Para cada tipo de partícula ha de tener un valor (en este caso, un valor restringido a múltiplos de 1/2), pero eso no nos dice por sí solo cuál es ese valor.
De todo lo dicho hasta ahora se deduce que la masa es una propiedad intrínseca de las partículas. Esa masa puede ser cero o distinta de cero. Aunque no sepamos por qué razón tiene el valor que tiene, no parece haber en principio ninguna contradicción en que sea distinta de cero.
Pero como ya dijimos, «la cosa no se queda ahí». En realidad, el problema de la masa es más serio que simplemente explicar por qué las partículas tienen la masa que tienen (sea cero o distinta de cero).
Como veremos en algún artículo futuro, es tremendamente difícil (aparentemente imposible) incorporar consistentemente un parámetro de masa distinta de cero para describir los electrones, quarks (y otras partículas) sin estropear otros hechos básicos. Y precisamente va a ser el bosón de Higgs, y el extraño mecanismo asociado a él, el que tenga la magia para resolver este problema.