En 1887, el rey Óscar II de Suecia (1829-1907) ofreció una recompensa peculiar: 2.500 coronas a la persona que resolviera la siguiente duda: ¿Es estable el Sistema Solar? Responder a la pregunta equivalía a descifrar el llamado “Problema de los tres cuerpos”.


El matemático Henri Poincaré aceptó el reto y se dio cuenta que se trataba de un problema irresoluble. De hecho, sólo se pueden obtener soluciones numéricas particulares… vamos, que sólo se puede resolver con un ordenador.
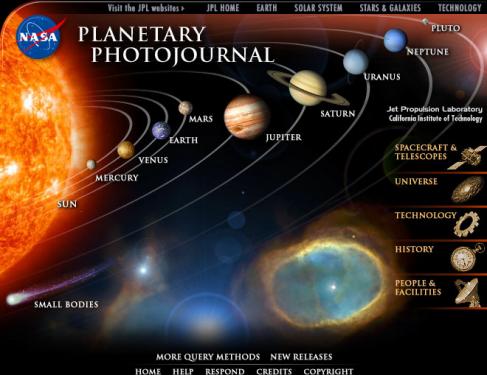
Estudiar la estabilidad del Sistema Solar nos lleva directamente a la ciencia del caos. Sabemos que las órbitas planetarias son caóticas, pero esto no quiere decir que los planetas acaben chocando unos contra otros, ya que tenemos un caos confinado.
En 1989, Jacques Laskar calculó las posiciones de los planetas hasta dentro de 150 millones de años. Sin embargo, sus cálculos demuestran una impredecibilidad intrínseca: cometer un error de sólo 15 metros a la hora de medir su posición actual hace imposible estimar dónde estará dentro de 100 millones de años.




Que fascinante es todo lo relacionado a la astronomía :-) ¿al final el rey le entregó el premio? al menos por intentarlo jeje
Sí se lo entregó a Poincaré, aunque nadie resolvió nada, creo que eligieron el que hiciera la mejor aportación científica, y Poincaré estableció algunas ideas que posteriormente llevaron a la Teoría del Caos.
Que interesante andrés….Que sepas,me encanta el mundo de la astronomía, me apasiona saber cosas qe están tan lejos pero a la vez tan cerca nuestra. Saludos , te seguiré leyendo todos los dias. :)
Me alegro que te gusten Alberto, yo también espero seguir leyendo tu blog.
Saludos.
Es extraño que todo lo que se encuentra sobre la estabilidad del sistema solar está basado en la teoría del caos. Las series de la mecánica celeste de Laplace no son convergentes, y las simulaciones por ordenador predicen catástrofes en un período no superior a 5 millones de años. Sin embargo, la realidad es que nuestro sistema solar ha sobrevivido más de 100 millones de años y las órbitas de los planetas, exceptuando Plutón, tienen una excentricidad minúscula.
Tanta casualidad es muy extraña, porque no se comprende que impacto tras impacto, perturbación tras perturbación, durante 100 millones de años, haya terminado por establecer órbitas tan circulares en todos los planetas. Demasiada casualidad, lo que demuestra que no es el caos lo que domina al sistema solar sino a la mecánica celeste, es decir, que debe de existir algo en la gravedad que todavía no se comprende, y que la materia oscura y la energía oscura no son los únicos misterios que siguen sin respuesta.
He encontrado un interesante artículo del físico Jaume Giné donde explica que una gravedad retardada justifica la misma rotación del perihelio de Mercurio que predice la relatividad general. Tampoco se encuentran más consecuencias de una gravedad retardada, de modo que yo mismo me tomé la molestia de programar una simulación, y los resultados demuestran que la excentricidad de las órbitas se corrige con el tiempo, de la misma forma que se regulan procesos físicos en lazo cerrado. Evidentemente, eso sí que explicaría las excentricidades tan pequeñas que se observan en las órbitas planetarias, a pesar de que existan perturbaciones.
Pero las curiosidades no terminan ahí. Si consideramos que la gravedad entre dos cuerpos depende de la relación entre sus masas, que se comportan como una cadena de dos eslabones cuya resistencia es la del eslabón más débil, resulta que la gravedad se refuerza a medida que la relación entre masas se acerca a la unidad. Esto no desentona con la gravedad en el sistema solar, y explicaría que exista más gravedad en las galaxias de lo que se deduce según la masa observable. Hay posibilidades prometedoras de que la materia oscura no exista, de que sea la gravedad la responsable de organizar el Universo en forma de filamentos, y de formar las barras y los brazos espirales de numerosas galaxias.
Más información sobre el tema y otros relacionados con la materia y las partículas puede encontrarse en http://origenmateria.blogspot.com.es/