En una reunión, se plantea este problema:
– Imaginemos que despegó de San Petersburgo un dirigible rumbo al norte. Una vez recorridos 500 km. en esa dirección, cambió de rumbo y puso proa al este. Después de volar en esa dirección 500 km., hizo un viraje de 90º y recorrió en dirección sur 500 km. Luego viró hacia el oeste, y después de cubrir una distancia de 500 km., aterrizó.
Si tomamos como punto de referencia San Petersburgo, se pregunta cuál será la situación del lugar de aterrizaje del dirigible: al oeste, al este, al norte o al sur de esta ciudad.
– Este es un problema para gente ingenua – dijo uno de los presentes -. Siguiendo 500 pasos hacia delante, 500 a la derecha, 500 hacia atrás y 500 hacia la izquierda, ¿adonde vamos a parar? Llegamos naturalmente al mismo lugar de donde habíamos partido.
– ¿Dónde le parece, pues, que aterrizó el dirigible?
– En el mismo aeródromo de San Petersburgo, de donde había despegado. ¿No es así?
– Claro que no.
– ¡Entonces no comprendo nada!
– Aquí hay gato encerrado – intervino en la conversación el vecino -. ¿Acaso el dirigible no aterrizó en San Petersburgo…? ¿Puede repetir el problema?
El aviador accedió de buena gana. Le escucharon con atención, mirándose perplejos, ya que nadie acertó la solución.
¿Dónde aterrizó el dirigible finalmente?
SOLUCIÓN en los COMENTARIOS

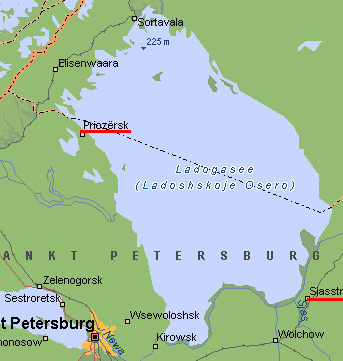





Este problema no tiene contradicción alguna. No hay que pensar que el dirigible vuela siguiendo el perímetro de un cuadrado; es necesario tener en cuenta la forma esferoidal de la Tierra.
Los meridianos, al avanzar hacia el Norte, se van aproximando; por ello, cuando vuela los 500 km. siguiendo el arco del paralelo situado a 500 km. al Norte de la latitud de San Petersburgo, el dirigible se desplaza hacia oriente un número de grados mayor que el que recorre después en dirección contraria, al encontrarse de nuevo en la latitud de San Petersburgo. Como resultado de ello, el dirigible, al terminar el vuelo, estaba al Este de San Petersburgo.
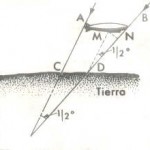
¿Cuánto? Esto puede calcularse. En la figura, se la ve la ruta seguida por el dirigible: ABCDE. El punto N es el Polo Norte; en ese punto se juntan los meridianos AB y CD. El dirigible voló primero 500 km. hacia el Norte, es decir, siguiendo el meridiano AN.
Como la longitud de un grado meridiano equivale a 111 km, el arco del meridiano de 500 km. contendrá 500 : 111 = 4 grados y medio. San Petersburgo está situado en el paralelo 50; por consiguiente, el punto B se encuentra en los 60º 4,5º = 64,5º. Después, el dirigible voló con rumbo Este, es decir, por el paralelo BC, y recorrió, siguiéndolo, 500 km.
La longitud de un grado en este paralelo puede calcularse y equivale a 48 km. Es fácil determinar cuántos grados recorrió el dirigible en dirección Este, 500 : 48 = 10,4º. Luego, la nave aérea tomó dirección Sur, es decir, voló siguiendo el meridiano CD y recorridos 500 km. había de encontrarse de nuevo en el paralelo de San Petersburgo.
Ahora la ruta toma dirección Oeste, es decir, va por AD; 500 km. de este camino es evidentemente una distancia más corta que AD. En la distancia AD hay los mismos grados que en la BC, es decir, 10,4º. Pero la distancia de un grado, a los 60º de latitud, equivale a a55,5 km. Por consiguiente, entre A y D existe una distancia igual a 55,5 x 10,4 = 577 km.
Vemos, pues, que el dirigible no podía aterrizar en San Petersburgo; le faltaron 77 km. para llegar a este punto, es decir, que descendió cerca del lago Ladoga.
No estoy de acuerdo para nada con la solución.
“la longitud de un grado meridiano equivale a 111 km”
Eso es un chiste??
El tipo que diseñó el problema se debía creer muy listo y lo es a la inversa, para empezar la distancia se mide en metros en el sistema internacional, y está perfectamente definida, y 1 Km son 1000 metros.
La solución sin embargo no es (o sí) tan trivial como se narra en el enunciado, depende del sistema de referencia que tomemos, no es lo mismo que consideremos como sistema de referencia el Sol, en cuyo caso hay que considerar la rotación de La Tierra o que tomemos como sistema de referencia La Tierra (ó San Petesburgo), lo que en cualquier caso queda descartado es considerar la distancia como grados meridianos.
Me parece que si dice «al norte», «Al sur», etc, la referencia son los polos. Por cierto, en ninguna parte veo que diga que un kilómetro sea diferente a 1000 metros, lo que indica es que la diferencia de un grado entre paralelos es de 111 Km.
Con un ejemplo se entiende: San Petersburgo se encuentra en el paralelo 59º 56′ 20.58″ N, si nos movemos un grado hacia el norte, a lo largo del meridiano, ese punto (con coordenadas 60º 56′ 20.58″ N) estará distante del primero aproximadamente 111 Km (los meridianos son los mismos en este ejemplo y es 30º 18′ 56.82″ E, estas coordenadas son aproximadamente del Palacio de Invierno)
Estoy de acuerdo con guerrero. Todo depende del punto de referencia. Es lo que se llama movimiento relativo, y depende del punto de referencia. Como bien dices JCFC el punto de referencia podria considerarse los polos, realmente no son los polos, ya que son dos puntos, es el centro de la tierra puesto que es un movimiento esferico y con un gran matiz, no se realiza sobre la superficie de la tierra, si no en la atmosfera(esta no gira con la tierra) por lo que tambien se deberia tener en cuenta la rotacion de la tierra. El planteamiento del problema junto con su solucion es correcto, quizas simplificado, ya que habria q tener en cuenta el movimiento de la tierra. no es lo mismo recorrer 500km en el polo norte que en pleno ecuador, o dicho de otra manera, el desplazamiento lineal no es igual al angular. el desplazamiento lineal va en funcion del radio, no solo del angulo, por lo que, como he dicho, en el polo norte, el radio (con punto de referencia:el eje de la tierra) es mucho menor que en el ecuador, por lo que un desplazamiento de 360 grados en ambos sitios no supone la misma distancia recorrida, o el mismo desplazamiento lineal. en un polo el desplazamiento es cero, mientras que en el ecuador ha recorrido la longitud de la tierra. Espero haberme explicado, un saludo
Aterriza al oeste de la ciudad. Mientras el dirigible hace su recorrido, la tierra (y por lo tanto la ciudad) se movieron hacia el este.