Difícilmente olvidaremos la Copa América del 2015. Hasta esa fecha, solo teníamos recuerdos amargos de este torneo continental, como los del cabezazo que el «Gato» Fernández le tapó al «Pato» Yáñez en los últimos minutos de la final del año 1979, o del balón débilmente despejado por el «Cóndor» Rojas en la final de 1987. Y como debimos esperar demasiado tiempo, la alegría nos llegó por partida doble, pues se repitió al año siguiente. En 2016, además, el mejor jugador del campeonato fue un chileno: Alexis Sánchez.

En 2015, en cambio, el puesto de figura del campeonato quedó desierto. Permítanme, entonces, llenar ese lugar vacante declarando como estrella del torneo a un ente inanimado, el juguete más querido por miles de niños, el regalo más esperado para cumpleaños y navidades: la pelota.
Confeccionar un balón de fútbol no es tarea sencilla, y lo era aun menos hace unas décadas. Nuestros mayores suelen decir que los jugadores de antaño eran mil veces mejores que los de ahora porque, entre otras cosas, debían patear pelotas varias veces más pesadas, de esas que dolía atajar o cabecear, especialmente cuando llovía.
Y mucho de eso es cierto, pues los primeros balones eran muy distintos a los actuales. La tecnología estaba recién desarrollándose, y se hacía muy difícil, por ejemplo, dar la última costura. Tan solo observe el siguiente diseño: así era la pelota del primer Mundial de Fútbol (1930), aquel cuya final enfrentó a Uruguay y Argentina y que Gardel «no quiso ver».

La geometría del diseño fue evolucionando lentamente. Durante décadas se usaron pelotas que eran híbridos entre el balón actual y uno de vóleibol. Entre ellas destacan la del Mundial de 1950 (esa que, en la épica jornada del Maracanazo, Ghiggia le clavó abajo a la izquierda a Barbosa: «Gol de Ghiggia Uruguay 1950» en YouTube) y, obviamente, la mítica Crack, la pelota del Mundial de 1962 (esa que, en Arica, Leonel Sánchez le clavó de zurda y borde externo a Yashin —la «Araña Negra»— al lado derecho: «WC 1962 Chile vs. USSR 2-1 (10.06.1962)» en YouTube).
En orden correlativo: los balones de los mundiales de 1930, 1934, 1938, 1950, 1954, 1958, 1962 y 1966.

En esta historia de pelotas, el Mundial de México 1970 (quizás el mejor de todos los tiempos) marcó un hito. Unos años antes, una serie de satélites de llamativa geometría habían sido puestos en órbita. En honor a ellos, el balón mundialista —diseñado por Adidas— fue llamado de la misma manera: Telstar. Con variaciones solo en la decoración y el nombre (Tango, Azteca, Etrusco, etcétera), este fue usado en todos los mundiales hasta el 2002, y sigue siendo hoy el más popular. La Cachaña, balón oficial de la Copa América 2015, obedece al mismo patrón, aunque consta de elementos anexos —por ejemplo, subdivisiones de cada cara hexagonal— muy interesantes.


A la izquierda: el primer satélite Telstar dio inicio a la era de las comunicaciones modernas. A la derecha: el balón Telstar con el que se disputó el Mundial de México 1970.
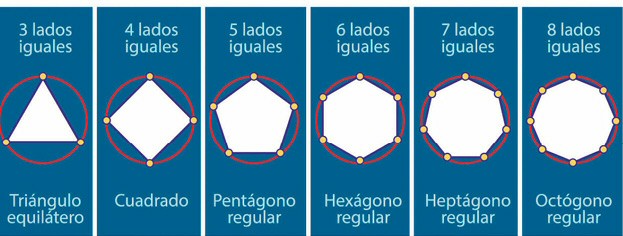
¿Cómo se diseña una de estas pelotas? Para responder a esta pregunta debemos remontarnos a los tiempos de los antiguos geómetras, quienes sabían muy bien que en el plano existen figuras perfectamente simétricas de cualquier número de lados. Tal como se observa abajo, estos «polígonos regulares» tienen bordes rectos, lados de la misma medida y ángulos iguales. Además, al girarlos sobre su centro en un ángulo apropiado caen nuevamente sobre sí mismos, al igual que si se los refleja ante un espejo bien dispuesto.
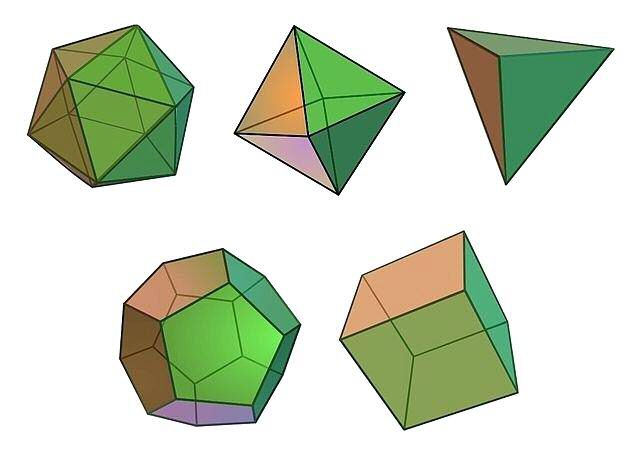
En nuestro espacio físico tridimensional ocurre, sin embargo, algo muy diferente. Por ejemplo, si intentamos armar un poliedro con siete caras y simetrías perfectas, constataremos rápidamente que esto es imposible. De hecho, hay solo cinco poliedros «regulares» convexos: el cubo, el tetraedro, el octaedro, el icosaedro y el dodecaedro, ilustrados en este orden más abajo. Si bien este es un descubrimiento del matemático ateniense Theaetetus, estos poliedros son llamados «sólidos platónicos» en honor al filósofo Platón, quien les atribuye un carácter «místico» en sus Diálogos.
¿Por qué solo cinco? Es fácil explicar por qué puede haber solo unos pocos: cada cara de un poliedro regular debe ser un polígono regular, y si se comienza con un polígono con muchos lados, entonces su ángulo interno será demasiado grande, lo cual nos dejará sin espacio suficiente para ensamblar otros polígonos y luego «cerrar» el poliedro.
Si los polígonos de las caras tienen m lados, entonces sus ángulos internos miden (m − 2)180°/m. La suma de los ángulos que concurren a cada vértice del poliedro debe ser inferior a 360°, para que así exista el espacio suficiente para acoplar los polígonos «hacia adentro». Por lo tanto, si en cada vértice concurren n polígonos, entonces se debe cumplir (m − 2)180°/m < 360.
Dividiendo por 180 cada lado de esta desigualdad, deducimos que n(m − 2) < 2m, es decir, nm < 2n + 2m, y por lo tanto, (n − 2)(m − 2) < 4.
Las únicas posibilidades para esto son las siguientes: n = 3, m = 4 (cubo); n = 3, m = 3 (tetraedro); n = 4, m = 3 (octaedro); n = 5, m = 3 (icosaedro) y n = 3, m = 5 (dodecaedro).
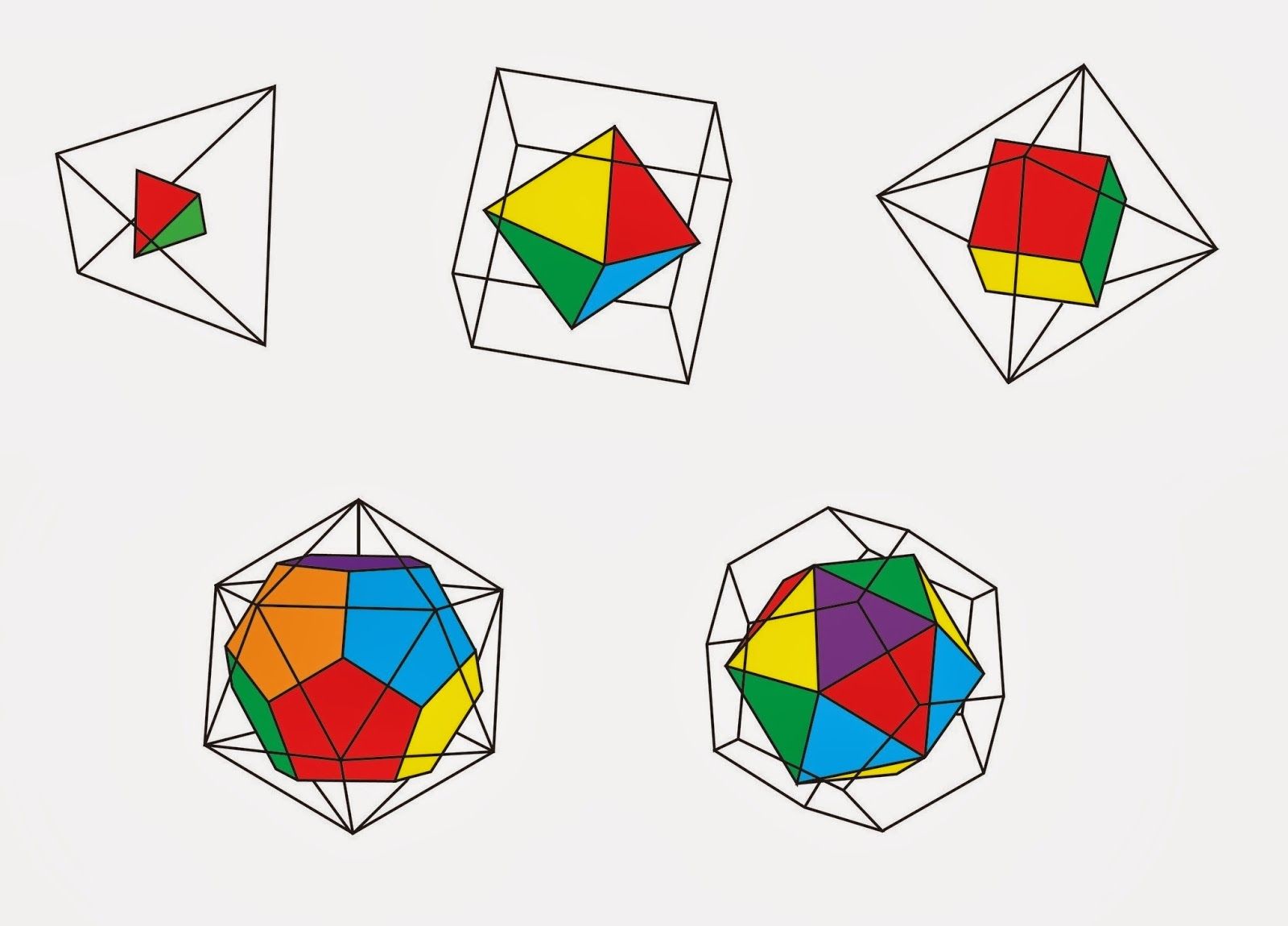
Los centros de las caras de un cubo son los vértices de un octaedro, y viceversa. Se dice entonces que el cubo y el octaedro son poliedros «duales». Los centros de las caras de un tetraedro son los vértices de un nuevo tetraedro; por lo tanto, este poliedro es dual a sí mismo. El dodecaedro y el icosaedro, por su parte, son duales uno del otro.
Los poliedros regulares y sus duales.
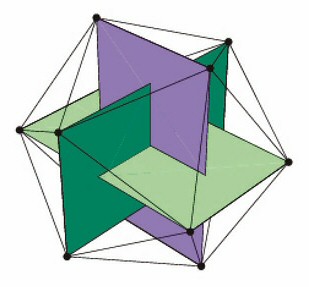
Los dos últimos poliedros están muy relacionados con la división áurea. Por ejemplo, los vértices de un icosaedro coinciden con los de tres rectángulos áureos (es decir, rectángulos en que la razón entre el largo y el ancho es igual a φ) que tienen el mismo centro y están dispuestos ortogonalmente unos con otros. Esta descripción explica el hecho de que, en coordenadas cartesianas, los doce puntos (0, ±1, ±φ), (±φ, 0, ±1) y (±1, ±φ, 0) son los vértices de un icosaedro.
Un icosaedro construido a partir de tres rectángulos áureos.
Debido a la rigidez espacial, que solo permite cinco formas perfectas, Arquímedes concibió otras combinando polígonos regulares de distinto número de lados. Si bien sus trabajos al respecto fueron muy detallados (llegando a describir las trece nuevas posibilidades), no fue sino hasta el Renacimiento cuando fueron redescubiertos, entre otros, por Johannes Kepler (el mismo que enunció las célebres tres leyes de la mecánica celeste).
Una forma de obtener un «sólido arquimediano» consiste en «truncar» un sólido platónico, es decir, cortar cada una de sus puntas mediante planos dispuestos de manera tal que todas las aristas resultantes tengan la misma longitud. Si realizamos este proceso con un icosaedro (y pintamos apropiadamente las caras), obtendremos la siguiente sugerente figura:
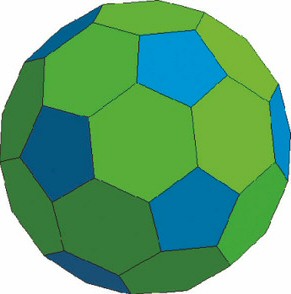
La pelota Telstar no es sino la versión esférica de un icosaedro truncado, en el que las veinte caras triangulares devienen hexágonos y doce caras pentagonales nacen de los vértices tras el truncamiento. Surge así la mítica configuración del «balón de los treinta y dos cascos» (y sesenta vértices).
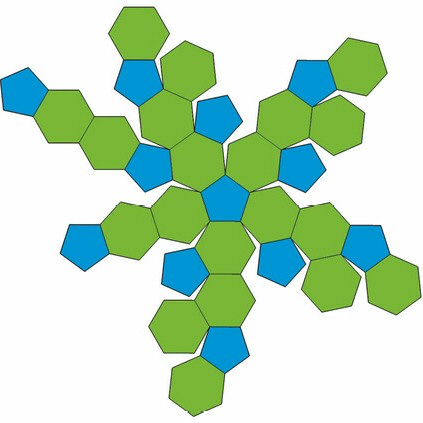
A continuación se ilustra un molde para hacer el icosaedro truncado (recuerde dejar unos pliegues para pegar las caras):
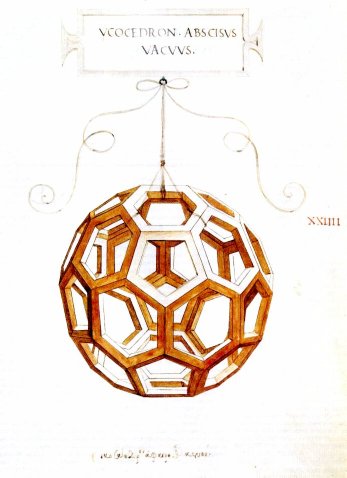
Pero no solo de pelotas vive el hombre. Las formas icosaédricas y dodecaédricas han maravillado a artistas desde tiempos remotos, tanto así que están presentes en la obra de Leonardo da Vinci (quien ya había imaginado una pelota Telstar inspirado en su naturaleza intrínsecamente áurea), de Salvador Dalí (quien representó su versión de La última cena en una bóveda dodecaédrica) y de muchos otros.
A la izquierda: una imagen de da Vinci en La divina proportione, de Luca Paccioli. A la derecha: La última cena, obra de Salvador Dalí.

Más tarde, en la década de los cuarenta, el inventor y arquitecto estadounidense Richard Buckminster Fuller creó sus famosos domos geodésicos, que hoy en día se han vuelto muy populares en nuestro país (especialmente en el Valle de Elqui y el Cajón del Maipo). Si bien estas son estructuras poliédricas de cierta regularidad, no corresponden a sólidos platónicos ni arquimedianos, aunque se parecen mucho a ellos.
Algunos comienzan con estructuras icosaédricas o dodecaédricas, las que son subdivididas apropiadamente en triángulos para conferirles mayor redondez y mejorar su resistencia sobre la base del principio de «tensegridad» (esto es, todas las piezas están sometidas a una cierta tensión, lo cual otorga estabilidad a la estructura). Sus caras, sin embargo, no siempre son polígonos regulares, y sus aristas tienen distintas medidas unas de otras.
Así, hacer los cálculos para construir un domo no es una tarea trivial. En páginas electrónicas de arquitectura se pueden encontrar programas para el «cálculo de domos», el cual se vuelve ligeramente más sofisticado cuando se pretende usar solo madera, sin «contaminar» la estructura con piezas metálicas (para este noble proceso, se deben calcular no solo las longitudes de las piezas, sino también sus ángulos de encaje).
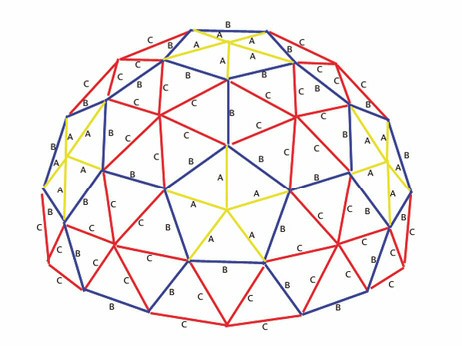
Sin duda alguna, el domo más famoso es el que sirvió de pabellón a Estados Unidos en la exposición universal de 1967 en Montreal, conocido hoy como la Biósfera y diseñado por el propio Fuller. El azar quiso que dos de las grandes innovaciones arquitectónicas ergonómicas, la de Fuller y la de Frei Otto, se hayan presentado al mundo en el mismo evento. Curiosamente, ambas tienen, además, alguna relación con el fútbol. Pero si Frei Otto exploró las posibilidades de la curvatura «negativa», Fuller sentó las bases de una arquitectura curvada «positivamente». El desarrollo de esta se extiende hasta el día de hoy, y nos ofrece maravillas como el Proyecto Edén en Grimshaw, Inglaterra. Inaugurado en 2001, se trata de un gigantesco jardín botánico poliédrico que tiene la virtud, además de estar confeccionado con materiales ligeros, de respetar el medio ambiente y aprovechar de manera espléndida la luz solar.
A la izquierda: la Biósfera de Montreal. A la derecha: el Proyecto Edén.


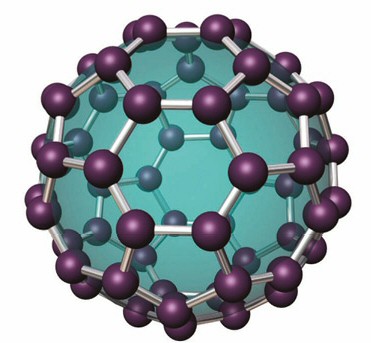
Pero esto no es todo. En 1985, Harold Kroto, Robert Curl y Richard Smalley descubrieron nuevos alótropos (formas moleculares estables) de carbono, distintas a los diamantes y al grafito, ya bien conocidos (este trabajo les valió el Premio Nobel de Química en 1996), a los que, debido a su configuración geométrica poliédrica, y en honor a Fuller, llamaron fullerenos.
En el más notable de ellos, el buckminsterfullereno (llamado también buckybalón o futboleno), cada molécula tiene la misma configuración de una pelota Telstar, lo cual se condice con su fórmula molecular: C60. Tiempo después, en plena era de la nanotecnología, nuevas formas serían descubiertas (por ejemplo, el grafeno), en una aventura científica que todavía está en plena efervescencia y ha dado origen a notables aplicaciones y promete aún muchas otras (entre las más espectaculares figura el rol inhibidor del fullereno para el virus del sida).
Una molécula de futboleno.
La historia de las formas poliédricas universales es apasionante. Al contemplar tanto desarrollo en torno a ellas, Platón muy probablemente hubiese mudado su visión mística de las cosas, olvidando sus famosos «cinco elementos» (tierra, fuego, aire, agua y éter, cada cual asociado a uno de sus sólidos) con los que pretendía explicar el universo. Así, se hubiese sumado a la tribuna para contemplar la maravilla de los domos geodésicos y de las microestructuras icosaédricas. Aunque, quizás, la armonía cósmica más prístina la hubiese hallado al patear una pelota Telstar en medio de una intensa pichanga en un descampado, o bien al contemplar el elegante juego de un genio rebelde del fútbol de ilustre nombre, muy inspirador para él: Sócrates.