Observad esta ilusión óptica. Por más que contéis los triángulos, veréis que son las mismas áreas tanto arriba como abajo. ¿Cómo es esto posible?
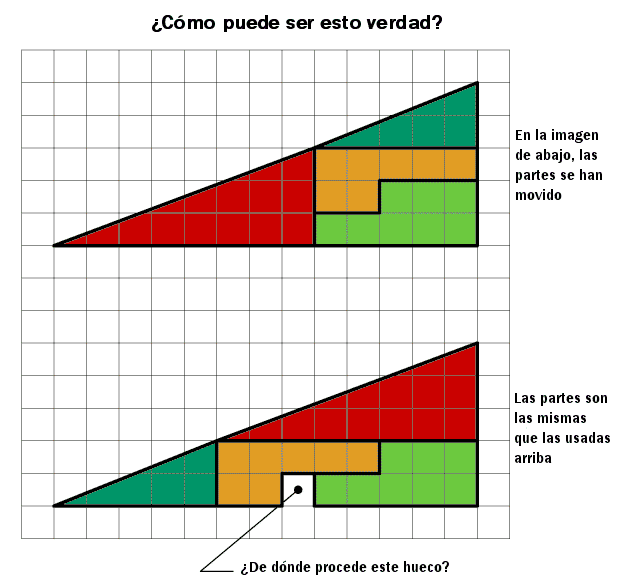
Por lo que he podido adivinar, al parecer no son exactamente triángulos con ángulos iguales, ya que el triángulo verde oscuro tiene un ángulo de 21.8º grados, mientras que el triángulo rojo posee 20.6º grados. Esa diferencia de 1.2º grados es imperceptible.
Para verlo más claro, he hecho unas líneas rectas sobre esos triángulos, haciendo coincidir el vértice de abajo, con la intersección del triángulo verde y el rojo. De esta manera, veis que en esa intersección, el triángulo de arriba está hundido y el de la imagen de abajo, está saliendo. Pero claro, es tan mínima la diferencia que apenas se nota, por eso es una ilusión óptica.
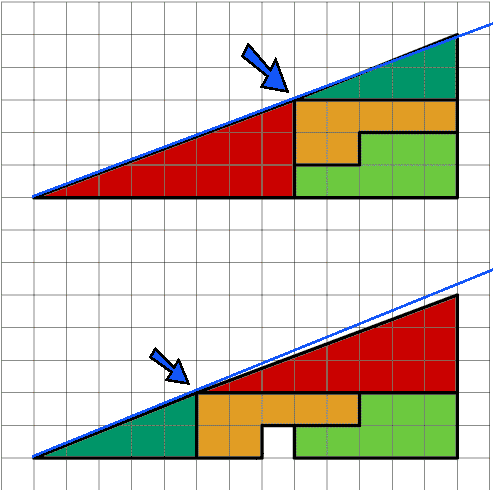
Así que en realidad, el gran triángulo que forman esas partes pequeñas, en realidad es un polígono.
Esto lo venden incluso como forma de puzzle. Ahora ya sabéis cómo resolverlo y porqué se forma.


Buenas tardes quisiera saber si ustedes tienen a la venta este puzzle y si si cual es el costo,y si tienen 200pzas.
Gracias
yo también vi la diferencia con tan solo observarlo
lo que lo hace cambiar es la posición de los triángulos rojo y verde azulado. si te fijas bien el cuadrado que «supuestamente falta» ¡no podría ser el 3 cuadradito de la primer fila de la derecha? (siempre dependiendo de la posición),sabiendo que la posición es incorrecta…
Andres espero tu respuesta , ya sea para corregirme o no
yo tuve que hacer uno ah escala para comprobarlo, y es peor de lo que pensé, los triángulos ni siquiera encajan como se ve en la figura, y no hay cambio de área, por que ni si quiera es como sale en esta imagen, seria bueno que lo compruebe cada uno por si mismo
gracias :)