Es muy probable que navegando en internet o consultando su cuenta de Facebook, usted se haya topado alguna vez con un intrigante video en el que se propone una forma de crear chocolate gratuitamente: «¡El Misterio del Chocolate Infinito Por Fin Revelado!» en YouTube. El método consiste, simplemente, en hacer unos cuantos cortes y reensamblar las partes, dejando fuera una de ellas.
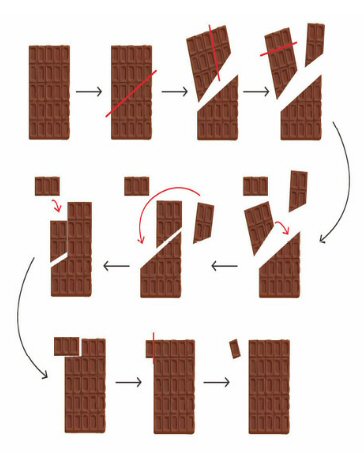
Claro está que algún truco debe haber, pues, como diría Lavoisier, «el chocolate no se crea ni se destruye, solo se transforma» (o se come). Lo que sucede es que tras cortar y reensamblar sin un cuadro, la barra se vuelve más corta, tal como se ilustra a continuación.
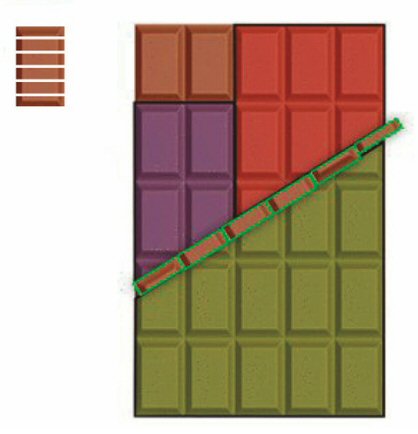
Una variación de este curioso truco aparece bosquejado abajo a la izquierda. Aquí, el problema son los ángulos, pues las líneas de las regiones roja y celeste no están sobre una misma recta, sino que se juntan formando ángulos distintos a 180°. Algo similar sucede en el bosquejo a la derecha.
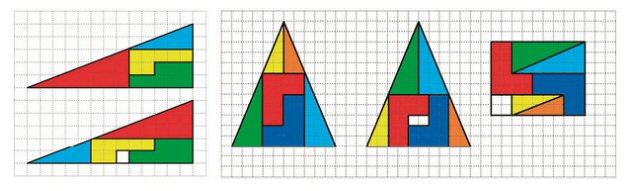
Lo anterior no es más que una deliciosa excusa para recordar que, aunque pueden parecer simples juegos, las acciones de cortar piezas, moverlas y reensamblarlas son facetas importantes de la geometría elemental. De ellas surge, por ejemplo, el famoso teorema de Pitágoras (el cual, dicho sea de paso, también aparece en manuscritos chinos de una época ligeramente anterior a la del sabio helénico).
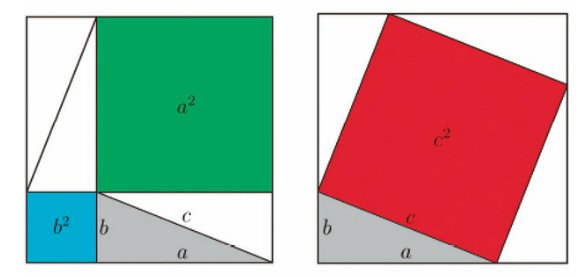
Seguramente usted conoce su clásico enunciado: «En todo triángulo rectángulo, la suma de los cuadrados de los catetos es igual al cuadrado de la hipotenusa». Pues bien, esta afirmación, que suele ser tristemente reducida a la oscura igualdad a2 + b2 = c2 resulta del hecho banal de que, al cortar astutamente los cuadrados construidos por sobre los catetos en unas pocas piezas, estas pueden ser reensambladas en el cuadrado construido sobre la hipotenusa, tal como se aprecia a continuación.
De manera alternativa, los cuadrados sobre los catetos pueden ser complementados por cuatro triángulos rectángulos en un cuadrado más grande, el cual puede ser llenado también con el cuadrado de la hipotenusa y los mismos cuatro triángulos. Expuesto de cualquiera de estas formas, el teorema más importante de la matemática de todos los tiempos no es más que un tangram, un simple juego de niños.
Muchos otros argumentos sencillos permiten probar el teorema de Pitágoras. Uno de ellos es obra nada menos que de Leonardo da Vinci, y otro del presidente de Estados Unidos James Garfield. En el sitio www.cut-the-knot.org/pythagoras/, hallaremos más de un centenar.
Siglos más tarde, esta faceta lúdica de la geometría (que no debe ser confundida con el «cortar y pegar» digital de los tiempos modernos) se concretizó en otro bello resultado que, lamentablemente, está ausente de nuestros programas educativos.
Se trata de un teorema descubierto en el siglo XIX y en forma independiente por el húngaro Farkas Bolyai, el prusiano Paul Gervien y el escocés William Wallace (¡atención!: este último no es el que lideró la independencia de su país, inmortalizado en la mítica película Corazón valiente).
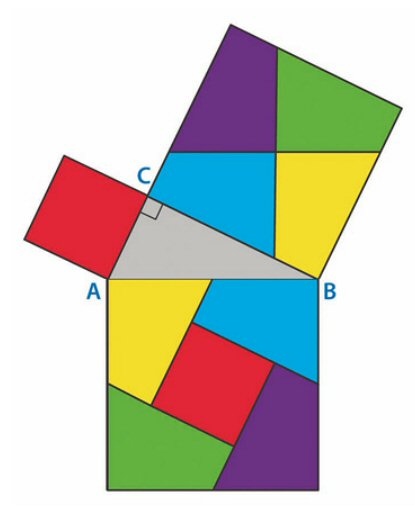
Este teorema establece que dadas dos figuras poligonales cualesquiera de igual área, siempre es posible cortar una de ellas a lo largo de un número finito de líneas rectas de modo que las piezas resultantes puedan ser reensambladas para obtener la otra.
Por ejemplo, en 1907, Henri Dudeney astutamente observó que existe una partición de un cuadrado en cuatro pedazos que, al ser dispuestos nuevamente, configuran un triángulo de la misma área y de lados iguales (esto es, un triángulo «equilátero»), tal como aparece ilustrado al inicio de este capítulo y está animado en YouTube: «Dudeneys Dissection». Cabe hacer notar, sin embargo, que esta brillante descomposición no es la única posible, aunque es la más sencilla que se conoce.
El argumento de Bolyai, Gervien y Wallace puede ser fácilmente implementado en situaciones concretas, como lo muestra el sitio interactivo http://dmsm.github.io/scissors-congruence. Así, guillotinando una esvástica (símbolo iconográfico de diversas culturas ancestrales, incluida la mapuche) y jugando con las piezas resultantes, podemos rápidamente formar una hermosa paloma.

He aquí otra preciosa fórmula de áreas (creada por el matemático austríaco Georg Alexander Pick) que data de 1899, pero que lamentablemente está ausente de nuestra bitácora escolar (aunque sería de gran utilidad para la PSU). Según Pick, si un polígono tiene «puntos enteros» como vértices (mejor dicho, puntos de coordenadas enteras), entonces su área es igual a la cantidad de puntos enteros en su interior menos uno, más la mitad de los puntos enteros que quedan en su borde:
Área = interiores − 1 + borde/2.
Si no lo cree, haga la prueba con las figuras expuestas abajo. Si se convenció, ahora resta saber por qué es cierta: en el número 1 del año 3 de la Revista del Profesor de Matemática hallará una demostración.
Hasta aquí solo nos hemos detenido a analizar figuras planas. Una interrogante surge entonces de manera natural: ¿puede hacerse algo similar con cuerpos geométricos tridimensionales? Sorprendentemente, esta pregunta inocente en apariencia resulta no ser tan sencilla.

Durante el Congreso Internacional de Matemáticos de París en los albores del siglo XX, David Hilbert, uno de los más destacados matemáticos de la historia, propuso una lista de veintitrés problemas que guiarían la investigación por los siguientes cien años. El tercer problema trataba precisamente sobre esta interrogante geométrica, y fue el primero en caer.
De hecho, la solución fue hallada apenas un par de años después por su estudiante Max Dehn, quien probó que es imposible hacer cortes rectos a un cubo de modo tal de obtener un número finito de piezas que, al ser redispuestas, configuren un tetraedro regular. Se desvanecía así un viejo anhelo, el de derivar de manera elemental las fórmulas de volúmenes de poliedros como, por ejemplo, aquella según la cual el volumen de una pirámide es igual a un tercio del producto del área de su base por su altura.
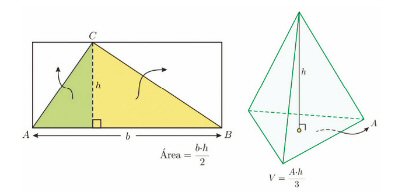
A la izquierda: el área de un triángulo es la mitad del producto de su base por su altura, pues coincide con la mitad del rectángulo correspondiente. A la derecha: la fórmula análoga del volumen de un poliedro no puede ser establecida por un método similar; la verificación de su validez requiere inexorablemente el uso del cálculo diferencial (o de alguna herramienta similar).
Más aun, Dehn logró entender exactamente cuándo un poliedro es equivalente a otro del mismo volumen por este proceso de corte y reensamblaje. En resumen, el espacio tridimensional resultó ser mucho más complejo que el plano.
¿Y si volvemos entonces al mundo bidimensional pero consideramos cortes no necesariamente rectos? En este contexto, nos encontramos cara a cara con una verdadera pesadilla de los matemáticos de la antigüedad: el problema de la cuadratura del círculo (esto es, construir, usando solo una regla —no numerada— y un compás, un cuadrado de área igual a la de un círculo dado). En la antigua Grecia se había hecho un progreso que se creía llevaría a su solución.
En efecto, aunque no se conserve ninguna de sus obras, se sabe que Hipócrates de Quíos (no confundir con Hipócrates de Cos, el padre de la medicina) había observado lo siguiente: si sobre la hipotenusa de un triángulo rectángulo de catetos iguales se construye una lúnula como en la figura siguiente, entonces su área es igual al área del triángulo.
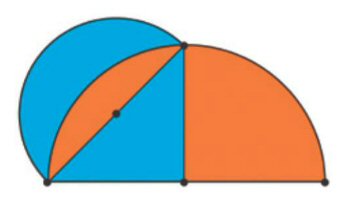
En la construcción de la lúnula de Hipócrates, la circunferencia externa debe estar centrada en el punto medio del cateto: las áreas pintadas de azul son iguales.
Esta configuración admite diversas variaciones, como la del sabio persa Alhacén. En ella, la suma de las áreas de las lúnulas construidas sobre los catetos es igual al área del triángulo. El punto crucial de esta configuración consiste en que la circunferencia cuyo diámetro es la hipotenusa pasa por el vértice del ángulo recto.
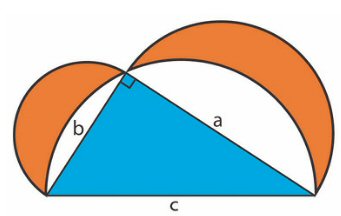
La suma de las áreas de las lúnulas naranjas (L1 y L2) es igual a la suma de las áreas de las semicircunfencias en a y b (Sa y Sb, respectivamente) menos la de la semicircunferencia Sc en c más el área Δabc del triángulo. En «fórmulas», esto es:
L1 + L2 = Sa + Sb − Sc + Δabc = πa2 + πb2 − πc2 + Δabc
Todas estas configuraciones maravillaron a Leonardo da Vinci, quien se obsesionó con el problema de la cuadratura del círculo y estaba convencido de que las lúnulas serían la herramienta decisiva para su solución. Sin embargo, en este punto da Vinci estaba equivocado, si bien la lápida a toda esperanza de cuadrar el círculo no vino a ser puesta sino cuatro siglos después por el matemático alemán Ferdinand von Lindemann.
Pobre da Vinci, murió creyendo en un imposible.